Deep Learningの定義は「4層以上のニューラルネットワーク」と定義されている。今回はDeepLearning4jの利用方法を確認する前に、ニューラルネットワークの概念について確認する。
■ ニューラルネットワークとは?
ニューラルネットワークとは、ニューロンが相互接続したネットワークのことを指す。ニューロンとは神経細胞のことを指し、人の体は相互接続されたニューロンのネットワークによって光を感じたり運動信号を伝達したりする。ニューロンを図示すると以下のようなものである。ニューロンの機能は、他のニューロンからの刺激を樹状突起を通じて受け取り、細胞核で処理したのち、軸索を通じて他のニューロンを刺激するというものである。
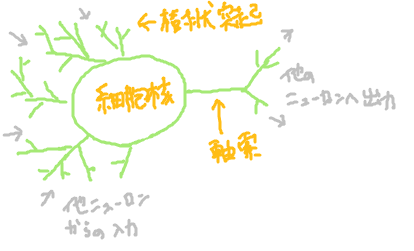
図:神経細胞のイメージ
ニューロン1つはとてもシンプルな構造だが、ネットワークを構築すると複雑な処理も可能にすることが知られている。このことに数学の世界が注目し、ニューロンのようなシンプルな構造を持つ関数のネットワークで複雑な関数を近似することができないかと考案されたのがニューラルネットワークという数理モデルである。数学の世界のニューロンは以下のような構造を持つ。

図:ニューロンのイメージ
\begin{align}
f(x) & = f( \sum_{i=0}^N v_ix_i - \theta )\\
& = f( v_0x_0 + v_1x_1 + \cdots + v_Nx_N - \theta )\\
\end{align}
つまり、入力は\(N\)個の他のニューロンからそれぞれ入力\(x_i\)に重み\(v_i\)を乗じた値の合計で、出力は入力から閾値\(\theta\)を引いて活性化関数\(f(x)\)で処理した値となる。このニューロンンをネットワーク上につなげたものをニューラルネットワークと呼ぶ。ニューラルネットワークを大きく分けるとニューロンを階層上に整列させる階層型と、そうでない非階層型に分かれる。非階層型としては内部にループ構造を持つものなどがあげられる。
一見、使い方がよく分からないニューロンではあるが、ニューロンを複数個つなげると利用方法が見えてくる。例えば以下のようにニューロンを構成すると、活性化関数\(f(x)=x\)という1次式だけを利用して、x>0の範囲で\(f(x)=x^2\)が近似できる。複雑な関数をシンプルな関数で表現できるという利点は、コンピュータでの計算を前提とすると大きな利点である。
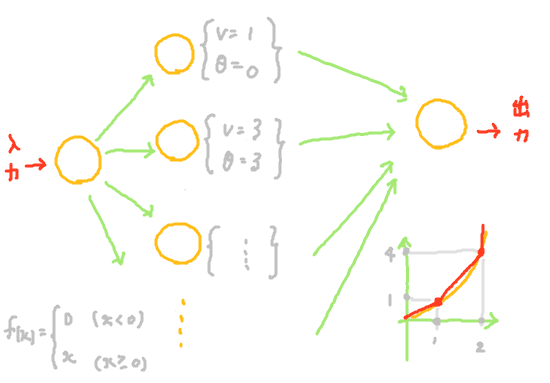
図:関数\(f(x)=x\)を用いて、ニューラルネットワーク上で関数\(f(x)=x^2\)を近似するイメージ
ニューラルネットワークでは上記のような簡単な式以外についても、活性化関数の選択やパラメータ\(v_i\)(重み)や\(\theta\)(閾値)の設定次第で、どんな関数も近似できるようになる。しかし、逆に問題となるのが式を近似する際にこのパラメータをどうやって求めるかということである。ニューラルネットワークにおいては、このパラメータの決定を次の節で紹介する学習により行っている。
■ 学習(誤差逆伝搬法)
機械学習という言葉が示すように、ニューラルネットワークにおいて学習という概念が最も大切な概念である。ただし、概念自体はそんなに難しいことはない。
例えば、中学で勉強した幾何学の世界を考えてみる。以下の問題でパラメータa,bを求めよと言われれば、求められるのではないだろうか。
【問題】
関数「\( y=ax+b\)」が点\((0,3)\)および点\((4,0)\)を通るとき、\(a\)と\(b\)の値を答えなさい。
【答え】
「\( 3=a \times 0+b \)」から\(b = 3\)、「\( 0=a \times 4+3 \) 」から\( a = -\frac{3}{4} \)
ニューラルネットワークにおいての学習は上記のようにパラメータ計算を行うことに相当する。上記の内容を一般的な言葉で置き換えると、入力\(x\)に対する出力\(y\)が分かっているのであれば、計算式中に現れるパラメータ(=適切な関数)が計算可能であるということである。上記の幾何学の問題を機械学習の観点で見てみると、入力に対応するデータの組「\((x,y)=(0,3),(4,0)\)」は教師データと呼ばれ、線形関数「\(y=ax + b\)」のパラメータ\(a\),\(b\)を計算することが学習にあたる。
もちろん、上記例のように関数が1次関数であれば瞬時に正確なパラメータが計算できるが、まったく未知の関数に対しては別の方法でパラメータを決定していく。それが、誤差関数の導入である。ここからは高校・大学レベルの数学知識が必要となる。
例えば、ある時点のニューラルネットワークの出力を\(o\)実際の正解値を\(t\)、誤差関数を\(E=(t-o)^2\)とすると、誤差関数は出力と正解値の差が小さくなるにつれて値が小さくなる関数となる。特に\(o=t\)の場合に誤差が最小となる。視覚的に誤差関数を記述すると以下のようになる。
図:誤差関数Eのイメージ
上記では、誤差関数Eをoの関数\(E(o)\)として表現したが、oはニューラルネットワークのパラメータである\(v_i\)や\(\theta\)によって決まる値であるため、誤差関数は\(E(v)\)や\(E(\theta)\)として記述することも可能である。ニューラルネットワークにおいては、この誤差関数を最小化するような\(v\)や\(\theta\)の値を求めることができれば、出力\(0\)と正解値\(t\)の差が小さい近似式を設定することができる。
この\(E(v)\)の最小値を求める方法として、ある時点での傾き(勾配)を調べるという方法がよく利用される。例えば\(E(v)=v^2\)という関数の最小値を求めることを考える。
図:\(E(v)=v^2\)のイメージ
いま適当な値\(v\)を決めて、\(v\)時点での\(E(v)\)の傾きを計算すると右下がりの傾き(負の傾き)であるとする。線の傾きはその点における微分値として計算することができる。線の傾きから、\(E(v)\)の最小値は\(v\)がより大きい値をとる場合であることが分かる。このため、次はvを少し大きくして\(v=v+\triangle v\)の地点に移動して、再度\(E(v)\)の傾きを計算する。この繰り返しを続けていけば、いつかは傾きが0=\(E(v)\)が最小になる\(v\)の値に収束する。この方法を数学的には再急降下法と呼ぶ。関数のある地点の傾きは関数の微分値に等しいことから、再急降下法では\(\triangle v= - \eta \frac{\partial E(v)}{\partial v} \)(\(\eta\)は定数)として無限に計算を繰り返す。
ニューラルネットワークにおいては、再急降下法のように勾配を利用して誤差関数\(E\)を最小化するようなパラメータ\(v\)や\(\theta\)を見つけることで式の近似を行っている。微分値を計算していくと、あるニューロンのパラメータ微分値(誤差情報)を計算する際には、その出力先のニューロンのパラメータ微分値が必要となるため、計算は出力側のニューロンから順に行われることになる。この動作が誤差情報が出力の流れとは逆に伝搬していくように見えることから、勾配を利用した学習の方法は誤差逆伝搬法と呼ばれる。
 図:誤差逆伝搬のイメージ
図:誤差逆伝搬のイメージ
■ 階層型ニューラルネットワーク
階層型ニューラルネットワークとは、ニューロンが階層上に重なったニューラルネットワークのことを指す。階層型ニューラルネットワークに属するものとしては、多層パーセプトロンや畳み込みニューラルネットワーク等が存在する。ネットワークのイメージとしては以下のようなものである。
図:階層型ニューラルネットワークのイメージ
近年注目を集めているDeep Learningは、この階層型ニューラルネットワークで入力層や出力層を合わせて全4階層以上の階層を持つものを利用した機械学習を指す。昔は処理が多すぎて見向きもされなかったが、近年のマシンスペックの向上に伴いその性能が見直されたモデルでもある。
■ 非階層型ニューラルネットワーク
非階層型ニューラルネットワークとは、ネットワーク内部にループを持つなど階層上になっていないニューラルネットワークのことを指す。非階層型ニューラルネットワークに属するものとしては、ボルツマンマシンなどが存在する。
図:非階層型ニューラルネットワークのイメージ
非階層型ニューラルネットワークの利用方法はイメージしにくいと思われるが、ボルマンマシンではニューロンを接続する線に適切な重みを設定することで、巡回セールスマン問題を解いたりグラフや図を記憶したりすることができる。
■ 参照
- 名古屋工業大学 岩田研究室 「ニューラルネットワーク入門」
