今回は、『
Javaで音声波形データを表示してみる』にて波形表示したwavファイルに対して、周波数分析(スペクトル解析)を行ってみる。周波数分析では離散フーリエ変換を利用するので、離散フーリエ変換についても簡単に確認する。
■ 周波数分析(スペクトル解析)
すべての波は正弦波の重ね合わせに分解できるということが周波数分析の基本となる。これだけ聞いたらフーンという程度なのだが、分解後の正弦波の周波数が分かるといろいろ便利なことに利用できる。例えば人の声の音声波形データを分解して得られるフォルマントという特徴量(周波数)の大きさを見れば、発音された母音・子音を判別できる(
*1)。また、JPEG画像やMP3音源データで利用されている離散コサイン変換は、膨大な波形データ配列(ピクセル値や振幅値)を少数の周波数配列に変換することにより大幅なデータ圧縮を実現している(
*2)。
このように波形データを複数の正弦波に分解することを周波数分析といい、分解された波の周波数分布をスペクトルという。また、連続的な時間のスペクトル変化を表したグラフをスペクトログラムという。スペクトログラムとスペクトルを視覚的に出力すると以下のようなものである。

 図:音声解析ソフトwavesurfer(*3)により出力されたスペクトログラム(左)と、スペクトログラム内のある時間(オレンジ色の線)におけるスペクタル(右)。それぞれ(横軸,縦軸)=(時間,周波数) , (周波数,パワースペクトル)を表す
図:音声解析ソフトwavesurfer(*3)により出力されたスペクトログラム(左)と、スペクトログラム内のある時間(オレンジ色の線)におけるスペクタル(右)。それぞれ(横軸,縦軸)=(時間,周波数) , (周波数,パワースペクトル)を表す
■ 離散フーリエ変換・逆離散フーリエ変換
「周期的なパターンを持つ関数(周期関数)は正弦波の重ね合わせで表現できる」と言ったのがかの有名なジョゼフ=フーリエ先生であり、先程述べた波の分解もこの言葉の中に含まれる。この考えを数式で表したのがフーリエ変換及び離散フーリエ変換である。フーリエ変換が連続関数を対象にしているのに対して、離散フーリエ変換は非連続(離散)関数を対称にしているが同等の内容である。コンピュータ上で扱う波形データは数の配列=非連続であるため、プログラミング上では離散フーリエ変換を利用することになる。
離散フーリエ変換(DFT)
離散フーリエ変換は以下の式で表される(正確に言うと離散フーリエ変換の式にオイラーの公式を適用した式である)(
*4,
*5,
*6)。N個の波形データのサンプルを取得し、以下の式にn番目のサンプルデータx
nを代入していくだけで、基本波のk倍の周波数成分の強さF
kを取得できる。基本波とはN個のサンプルを取得した期間を1周期とする波のことを表す。

F
k = Σ
N-1n=0 x
n( cosθ - i * sinθ )
θ = 2πnk / N
◇変数説明
|
|
| N |
:サンプルデータ数 |
| Fk |
:基本波のk倍の周波数を持つ波の強さ。(0<= k < N )
複素数(a + bi)の形で取得できる |
| xk |
:k番目のサンプルデータ |
| i |
:虚数単位( i2=-1のアレ) |
◇使用前提
1.周期関数であること
2.線形システムである(解の重ね合わせが成り立つ)こと
*解の重ね合わせ…f(x)の解がa,bであるとき、αa +βbもまた解である(*7)
数式内に虚数が出てきているので少し驚くが、1つの数式中に2つの次元(sin=偶関数とcos=奇関数)を同居させるために使っているだけなので実数部と虚数部を分けて考えることだけ覚えておけばよい(
*8)。
数式の利用には少し気をつけないといけない。1つめは基本波のn倍の周波数成分を扱いたい場合は、サンプリング点数Nを2n点以上にする必要がある点である。これは標本化定理の話で、もし2n点以上にしなかった場合はエイリアジングという現象が発生し、正確な周波数成分が取得できなくなる。
更に数式の利用前提条件1に関連して、正確な周波数成分を出したければ離散フーリエ変換で利用するサンプルは周期信号の1周期分となっていないといけないことがあげられる。また、離散フーリエ変換では基本波の整数倍の周波数成分に分解するため、それ以外の周波数帯の波は整数倍の波の周波数成分に分割して乗っかるということも考慮にいれる必要があるとのこと(
*9)。まあ、離散フーリエ変換で出力される値はいつも正確な周波数成分値ではないということを頭に入れておけということですね。
離散フーリエ変換を実装してみると分かると思われるが、計算量が多くなることが欠点の1つである。このため高速化アルゴリズムとして高速フーリエ変換(FFT)という数式が発明されている。サンプルデータ数Nが2のべき乗個である場合にのみ利用できるアルゴリズムであり、たいていのソフトウェアではこの高速フーリエ変換が利用される。
短時間フーリエ変換(STFT)
離散フーリエ変換ではサンプルデータが周期信号になっていないといけないという条件があった。このため、サンプルデータの最初(0番目サンプル)と最後(N番目サンプル)の値が連続でないと正確な値は出てこない。この制限を緩めるために窓関数という関数を利用しするのが短時間フーリエ変換である(
*10)。
窓関数とはガウス関数のように両端が0で中央付近が1となる関数である(
*11)。この窓関数をサンプルデータに適用すると両端の値が0になり連続値となるため、離散フーリエ変換の精度が上がるのである。スペクトログラムの作成など、短期間のデータを元に離散フーリエ変換を行う際には、周期信号でない場合が多いためよく利用される。
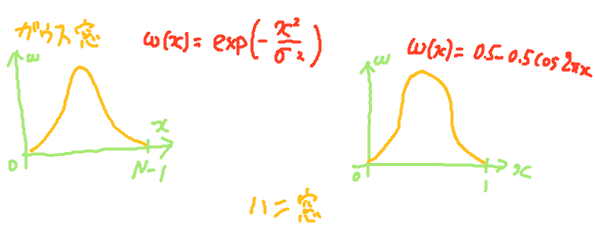 図:窓関数の例:関数の形と計算コストからハン窓が利用されることが多い模様
図:窓関数の例:関数の形と計算コストからハン窓が利用されることが多い模様
逆離散フーリエ変換
離散フーリエ変換は線形変換(1次関数)であるため逆変換が可能である。逆離散フーリエ変換の数式は以下で表される。基本的に離散フーリエ変換と同じであるが、振幅値を調整するためサンプルデータ数Nで除算する必要がある。
xk = 1/N * Σ
N-1n=0 F
n( cosθ - i * sinθ )
θ = 2πnk / N
◇変数説明
|
|
| N |
:サンプルデータ数 |
| Fk |
:基本波のk倍の周波数を持つ波の強さ。(0<= k < N )
複素数(a + bi)の形で取得できる |
| xk |
:k番目のサンプルデータ |
| i |
:虚数単位( i2=-1のアレ) |
■ 実装プログラム
以下にwavファイルから音声波形を取り出し、離散フーリエ変換を行うプログラムを示す。プログラムでは、以下の情報を出力している。
- 元音声波形データ
- 離散フーリエ変換後の音声周波数(スペクトル)の実数部
- 離散フーリエ変換後の音声周波数(スペクトル)の虚数部
- 逆離散フーリエ変換で復元した音声データ波形
◇リソース
music/dog01.wav(提供元:
フリー素材 -SpiderWorks-サイト内の
動物系効果音『犬1』)
◇サンプルプログラム
package application;
import java.io.File;
import java.nio.ByteBuffer;
import java.nio.ByteOrder;
import javax.sound.sampled.AudioFormat;
import javax.sound.sampled.AudioInputStream;
import javax.sound.sampled.AudioSystem;
import javafx.application.Application;
import javafx.scene.Node;
import javafx.scene.Scene;
import javafx.scene.chart.LineChart;
import javafx.scene.chart.NumberAxis;
import javafx.scene.chart.XYChart;
import javafx.scene.chart.XYChart.Series;
import javafx.scene.layout.HBox;
import javafx.scene.layout.VBox;
import javafx.stage.Stage;
/**
* 音声(wav)データの波形を見るプログラム
* ただし、Wav(PCM・リトルエディアン)形式で保存された
* ファイルのチャンネル1のみ出力
*
* @author karura
*
*/
public class TestWaveSpectrum extends Application
{
// 定数
private final String fileName = "music/dog01.wav"; // チャートに表示する音声ファイルへのパス
private final double sec = 0.15; // チャートに表示する期間(s)
// 取得する音声情報用の変数
private AudioFormat format = null;
private double[] valuesActual = null;
private double[] valuesImaginal = null;
private double[] spectrumActual = null;
private double[] spectrumImaginal = null;
public static void main(String[] args) {
launch(args);
}
@Override
public void start(Stage primaryStage) throws Exception
{
// フォント色がおかしくなることへの対処
System.setProperty( "prism.lcdtext" , "false" );
// シーングラフの作成
HBox root = new HBox();
VBox box1 = new VBox();
VBox box2 = new VBox();
root.getChildren().addAll( box1 , box2 );
// 音声データを読込
System.out.println( "loading wav data..." );
initialize();
// 元音声波形をチャート表示
box1.getChildren().add( createLineChart( "音声波形" , valuesActual ) ); // 折れ線グラフの追加
// 離散フーリエ変換後の波形をチャート表示
System.out.println( "caliculating DFT..." );
spectrumActual = new double[ valuesActual.length ];
spectrumImaginal = new double[ valuesActual.length ];
DFT( valuesActual , spectrumActual , spectrumImaginal , false );
// 離散フーリエ変換後のスペクトルをチャート表示
box2.getChildren().add( createLineChart( "スペクトル(実数部)" , spectrumActual ) ); // 折れ線グラフの追加
box2.getChildren().add( createLineChart( "スペクトル(虚数部)" , spectrumImaginal ) ); // 折れ線グラフの追加
// 逆離散フーリエ変換
System.out.println( "caliculating IDFT..." );
for( int i=0 ; i<valuesActual.length ; i++ )
{
valuesActual[i] = spectrumActual[i];
valuesImaginal[i] = spectrumImaginal[i];
}
IDFT( valuesActual , valuesImaginal , spectrumActual , spectrumImaginal );
// 逆フーリエ変換後のスペクトルをチャート表示
box1.getChildren().add( createLineChart( "逆フーリエ変換後の音声波形" , spectrumActual ) ); // 折れ線グラフの追加
// シーンの作成
Scene scene = new Scene( root , 800 , 400 );
// ウィンドウ表示
primaryStage.setScene( scene );
primaryStage.show();
}
/**
* 音声ファイルを読み込み、メタ情報とサンプリング・データを取得
* @throws Exception
*/
protected void initialize() throws Exception
{
// 音声ストリームを取得
File file = new File( fileName );
AudioInputStream is = AudioSystem.getAudioInputStream( file );
// メタ情報の取得
format = is.getFormat();
System.out.println( format.toString() );
// 取得する標本数を計算
// 1秒間で取得した標本数がサンプルレートであることから計算
int mount = (int) ( format.getSampleRate() * sec );
// 音声データの取得
valuesActual = new double[ mount ];
valuesImaginal = new double[ mount ];
for( int i=0 ; i<mount ; i++ )
{
// 1標本分の値を取得
int size = format.getFrameSize();
byte[] data = new byte[ size ];
int readedSize = is.read(data);
// データ終了でループを抜ける
if( readedSize == -1 ){ break; }
// 1標本分の値を取得
switch( format.getSampleSizeInBits() )
{
case 8:
valuesActual[i] = (int) data[0];
break;
case 16:
valuesActual[i] = (int) ByteBuffer.wrap( data ).order( ByteOrder.LITTLE_ENDIAN ).getShort();
break;
default:
}
}
// 音声ストリームを閉じる
is.close();
}
/**
* 離散フーリエ変換
* @param in フーリエ変換を行う実数配列
* @param outActual 計算結果の実数部配列
* @param outImaginal 計算結果の虚数部配列
* @param winFlg 窓関数の使用フラグ
*/
protected void DFT( double[] in , double[] outActual , double[] outImaginal , boolean winFlg )
{
// 配列初期化
int length = in.length;
// 離散フーリエ変換
for( int k=0 ; k<length ; k++ )
{
// 初期化
outActual[k] = 0.0d;
outImaginal[k] = 0.0d;
// 計算
for( int n=0 ; n<length ; n++ )
{
// 入力値に窓関数を適用
double normal = ( !winFlg )? in[n] : hanWindow( in[n] , n , 0 , length );
// k次高周波成分を計算
outActual[k] += normal * Math.cos( 2.0 * Math.PI * (double)n * (double)k / (double)length );
outImaginal[k] += -1.0 * normal * Math.sin( 2.0 * Math.PI * (double)n * (double)k / (double)length );
}
// 残りの計算
//outActual[k] /= length;
//outImaginal[k] /= length;
}
}
/**
* 逆離散フーリエ変換
* @param inActual 逆離散フーリエ変換を行う値の実数部配列
* @param inImaginal 逆離散フーリエ変換を行う値の虚数部配列
* @param outActual 計算結果の実数部配列
* @param outImaginal 計算結果の虚数部配列
*/
protected void IDFT( double[] inActual , double[] inImaginal , double[] outActual , double[] outImaginal )
{
// 配列初期化
int length = inActual.length;
// 離散フーリエ変換
for( int k=0 ; k<length ; k++ )
{
// 初期化
outActual[k] = 0.0d;
outImaginal[k] = 0.0d;
// 計算
for( int n=0 ; n<length ; n++ )
{
// k次高周波成分を計算
outActual[k] += inActual[n] * Math.cos( 2.0 * Math.PI * (double)n * (double)k / (double)length )
- inImaginal[n] * Math.sin( 2.0 * Math.PI * (double)n * (double)k / (double)length );
outImaginal[k] += inActual[n] * Math.sin( 2.0 * Math.PI * (double)n * (double)k / (double)length )
+ inImaginal[n] * Math.cos( 2.0 * Math.PI * (double)n * (double)k / (double)length );
}
// 残りの計算
outActual[k] /= length;
outImaginal[k] /= length;
}
}
/**
* 窓関数(ハン窓)
* @param in 変換する値
* @param i 配列中のインデックス
* @param minIndex 配列の最小インデックス
* @param maxIndex 配列の最大インデックス
* @return
*/
protected double hanWindow( double in , double i , double minIndex , double maxIndex )
{
// 入力値の正規化
double normal = i / ( maxIndex - minIndex );
// ハン窓関数の値を取得
double han = 0.5 - 0.5 * Math.cos( 2.0 * Math.PI * normal );
return in * han;
}
/**
* 折れ線グラフで波形表示
* @param title グラフのタイトル文字
* @param values グラフに出力するデータ配列
* @return 作成したグラフノード
*/
@SuppressWarnings("unchecked")
protected Node createLineChart( String title , double[] values )
{
// 折れ線グラフ
NumberAxis xAxis = new NumberAxis();
NumberAxis yAxis = new NumberAxis();
LineChart<Number, Number> chart = new LineChart<Number, Number>( xAxis , yAxis );
chart.setMinWidth( 400 );
chart.setMinHeight( 200 );
// データを作成
Series< Number , Number > series1 = new Series<Number, Number>();
series1.setName( title );
for( int i=0 ; i<values.length ; i++ )
{
series1.getData().add( new XYChart.Data<Number, Number>( i , values[i] ) );
}
// データを登録
chart.getData().addAll( series1 );
// 見た目を調整
chart.setCreateSymbols(false); // シンボルを消去
series1.getNode().lookup(".chart-series-line").setStyle("-fx-stroke-width: 0.75px;"); // 線を細く
return chart;
}
}
◇実行結果
 ◇解説
◇解説
プログラムの骨子はstart関数(48行目~96行目)に記述されており、initialize関数(62行目)でwavファイルを音声波形データとして読み込み、DFT関数(71行目)で離散フーリエ変換を行って音声波形データを周波数成分に分解、最後はIDFT関数(84行目)で逆離散フーリエ変換で音声データを復元している。またそれぞれの計算が終了した時点で、createLineChart関数(65行目、74行目、75行目、87行目)を用いて音声波形データと周波数成分を棒グラフとして出力している。
各関数の実装は数式に表されたとおりに計算を実施している。注意点としては、窓関数をhanWindow関数(225行目~234行目)を宣言し169行目で使用できるようにしているが、DFTの引数winFlg(153行目)としてはfalseで呼び出しているために今回のプログラムでは窓関数が一度も呼び出されない点である。
出力結果を見てみる。パワースペクトルは「{(Fの実数部の2乗)+(Fの虚数部の2乗)}の平方根」の形で計算されるので常に正の値だが、このプログラムはFの実数部と虚数部をそのまま出力しているため負の数も出力される。
該当のwavファイルの周波数成分を見ると、基本波の0~1200倍の周波数成分に集中しており、50~100倍の周波数成分が特に強いことが見て分かる。これを周波数に直すと基本波の波長が0.15秒(34行目)なので「1 / 0.15 * 50 = 333.3Hz」~「1 / 0.15 * 100 = 666.6Hz」の波となり、
前記事で調べた「ミの周波数=329.6Hz」「ファの周波数=349.2Hz」あたりの音が強いことになる(ハズ)。聞き比べるとなんとなくあっているような気もするが、よくわからない。ちなみに、5000倍以上の箇所にもデータが見えるが、「1 / * 0.15 * 5000 = 33333.3 Hz 」となりサンプリング周波数44100Hzの半分以上の周波数となっているため雑音データである。
周波数成分から逆離散フーリエ変換で復元した音声波形を見てみると、若干形が変わっている気もするが概ねうまく復元できている。こちらはよく分かる。
■ 参照
- 国語音声学 声紋を読んでみよう!
- Wikipedia 「離散コサイン変換」
- Source Forge 「wavesurfer」
- Energychord「離散フーリエ変換入門」
- Wikipedia 「離散フーリエ変換」
- Wikipedia 「オイラーの公式」
- コトバンク 「重ね合せの原理」
- 教えてgoo 「離散フーリエ変換(DFT)の実数と虚数」
- nabeの雑記帖 「FFTとは? ~本当は正しくないFFTの周波数特性~」
- Wikipedia 「短時間フーリエ変換」
- Wikipedia 「窓関数」
